Benchmarks¶
Introduction¶
One of the key questions for picking up Shark in your work is: “Is it fast enough?”. As Shark is not a black-box algorithm-toolbox, we often can not choose the implementation with maximum speed as we have to balance the speed requirements with flexibility. Nevertheless, if the resulting penalty is so large that practical application becomes impossible we would still regard it as a buggy implementation. Thus, we want to compare Shark to other, well known libraries and show timings in setups which are as similar as possible.
For now we compare Shark only with SciKit-Learn which often relies on well known and optimized C-code (libLinear and LibSVM for example) as well as cython and ATLAS for the heavy lifting.
We decided to compare a subset of algorithms with high practical relevance in daily work: Random Forrst, Nearest-Neighbours, Linear Regression, Linear- and Kernel-CSVM and Logistic Regression. This subset gives a good comparison of the quality of a wide range of implemented algorithms, from tree methods to Quadratic Programming. In cases where this makes a difference, we also compare dense and sparse inputs.
The implementations can be found in the Examples/Benchmark directory.
Datasets¶
We use the following datasets in the experiments:
Cod-Rna, which has 60k samples and 8dim data. rcv1.binary, which has 20k samples and high dimensional sparse data. MNIST, which has 60k samples and 768dim data. BlogFeedback, which has 60k samples and 281dim data for regression.
We ensure in all our experiments that all datasets except rcv1.binary are read in as dense to ensure the maximum possible efficiency.
Kernel-CSVM¶
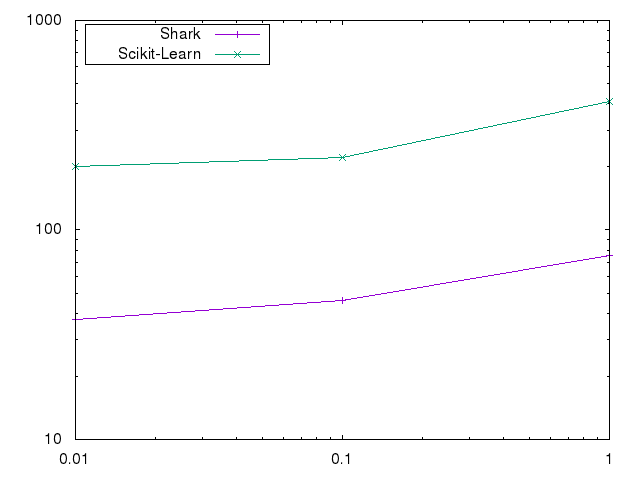
We used a radial Gaussian kernel with gamma=1 on the cod-rna dataset. We solve to an accuracy of 0.001 and vary C between 0.01 to 1 while fixing the kernel cache to 256MB.
The large difference are caused by the fact that Shark uses blockwise parallel evaluations of the kernel, while libSVM as used by Scikit-Learn does not.
Linear-CSVM¶
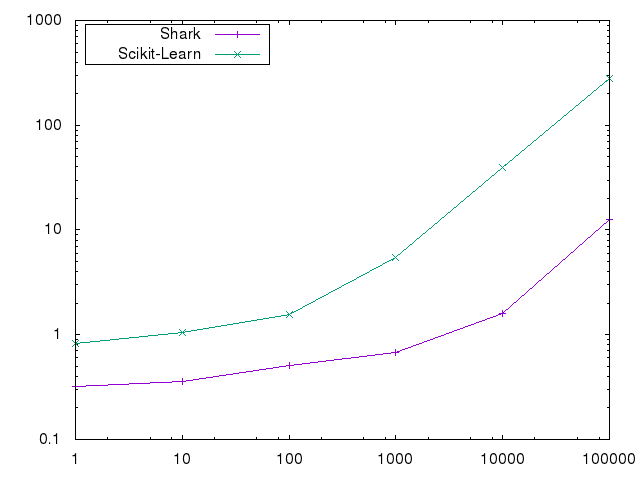
We used the rcv1.binary dataset. We solve to an accuracy of 0.001 and vary C between 1 and 100000. We do not use a bias in these experiments.
The differences are not caused by an implementation difference but by algorithmic improvements over LibLinear, which require much less iterations to reach a desired accuracy.
Logistic Regression¶
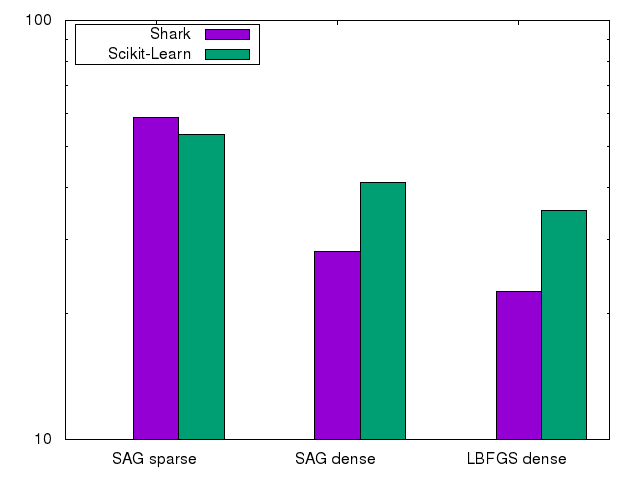
We used two algorithms here: an LBFGS based optimizer on the multi-class MNIST dataset as well as an SAG optimizer on the even-vs odd MNIST and rcv1.binary datasets. In our experiments we chose alpha=0.1. The SAG optimizer is a good example where Shark has to be slower than a specialized implementation. Shark needs to spend additional function evaluations to adapt the learning rate while Scikit-Learn can choose a good one from the start as it knows which loss functions to expect. Also note that in the LBFGS case the Shark implementation uses the abstract optimizer and objective function framework instead of a specialized solver.
Nearest-Neighbours¶
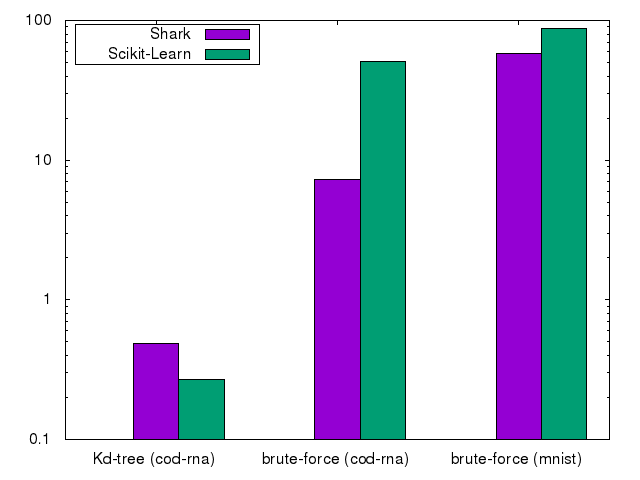
We use a Kd-tree based algorithm on the low-dimensional cod-rna and compare it to the same brute-force algorithm. We also use MNIST to compare the brute-force algorithm on high dimensional data. We use k=10 nearest neighbours in all experiments.
Others¶
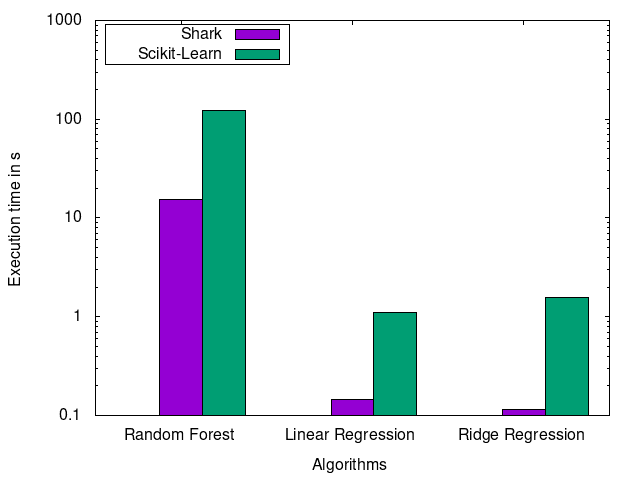
Finally, we compare random forests on cod-rna, and logistic and ridge-regression on BlogFeedback.

